Some Integrals

A typical Calculus student will know that an integral is the “reverse” of a derivative, and is used in finding the area enclosed by lines and curves alike. While I’m not an official student of the said subject, I had some little experiences with integrals, and I shall be happy to share some of the problems I’ve answered with you. I’ll post three problems here: the first is solved using partial fractions, the second through double-IBP, while the last is a bit “improper.”

First Problem: ∫ 1/(9 – y²) dx

Do you still recall the difference of squares from algebra? If you do, then you should recognize that 9 – y² can be factored to (3 + y)(3 – y). In this case, partial fractions seem to be the best method to solve this thing. In partial fraction decomposition, we break down a rational expression to two or more rational expressions, where each factor of the original expression’s denominator gets its own fraction with an unknown numerator. Hence, we have:

1/(9 – y²) = A/(3 + y) + B/(3 – y)

We’re now aiming to find A and B. To make things easier, distribute the LCD to get rid of the denominators.
1 = A(3 – y) + B(3 + y)

Let y = -3 to find A.                               Let y = 3 to find B.
1 = A(3 -(-3)) + B(3 – 3)                        1 = A(3 – 3) + B(3 + 3)
1 = 6A                                                   1 = 6B
1/6 = A                                                  1/6 = B

Hence, we now have this new integrand.
∫ 1/6 /(3 + y) +  1/6 /(3 – y) dx

Factor out the constants to make integration easier.
1/6 ∫ 1/(3 + y) dx + 1/6 ∫ 1/(3 – y) dx

You can confirm through u-substitution that our integral would be:
(1/6)ln|3 + y| + (1/6)ln|3 – y| + C (Answer)

Second Problem:
∫ ln²x / x² dx

U-substitution won’t work here, obviously. The numerator is too complex, so partial fraction decomposition won’t work too. We’ll have to use IBP, or integration by parts. First, let’s make some substitutions.

u = ln²x or (ln x)²      dv = 1/x² or x⁻²
du = 1/x . 2ln(x) dx     v = -x⁻¹

Let’s start solving!
∫udv = uv – ∫vdu
∫ln²x / x² = -ln²x/x – ∫ -2ln(x) / x² dx
= -ln²x/x + 2 ∫ ln(x) / x² dx

The integrand seems to be still complicated, so we’ll have to use IBP again.
u = ln(x)    dv = 1/x² or x⁻²
du = 1/x dx   v = -x⁻¹

= -ln²x/x + 2[uv - ∫vdu]
= -ln²x/x + 2[-ln(x)/x - ∫ -1/x²]
= -ln²x/x + 2[-ln(x)/x + ∫ 1/x²]

We can now integrate quite easily.
= -ln²x/x + 2[-ln(x)/x - 1/x] + C
= -ln²x/x – 2ln(x)/x – 2/x + C (Answer)

We’re on the final problem. The answers to the first two problems are called indefinite integrals, because they aren’t evaluated at some upper limit b and lower limit a. Now, however, we’re going to solve for a definite integral, with a twist.

∫[0 to ∞] r²(exp(-r)) dr

The actual format of the problem is:



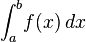
Alright. Let’s start off with a little manipulation of the problem. exp(n) is also eⁿ. So we have:
∫[0 to ∞] r² . e⁻ʳ dr

We can integrate the expression, but we can’t simply evaluate the integral to the given limits normally. Infinity being the upper limit is the one that complicates things. This peculiar problem is an example of solving “improper integrals.”

The first step to make this problem solvable is to replace the ∞ limit with any variable. I want to use Ω. The next step is to take the limit of the integral as Ω approches infinity. Therefore, we have this new problem.

lim ∫[0 to Ω] r² . e⁻ʳ dr
Ω→∞

Ignore the lim something for a while. Let’s focus on the integrand. Judging by the looks of it, I say, use integration by parts!
u = r²      dv = e⁻ʳ
du = 2r dr    v = -e⁻ʳ

∫udv = uv – ∫vdu
∫r² . e⁻ʳ = -r²e⁻ʳ – ∫ -2r.e⁻ʳ dr
= -r²e⁻ʳ + 2∫re⁻ʳ dr

Since the integrand is still complicated, we should apply IBP one more time.
u = r     dv = e⁻ʳ
du = dr    v = -e⁻ʳ

= -r²e⁻ʳ + 2[uv - ∫vdu]
= -r²e⁻ʳ + 2[-re⁻ʳ - ∫-e⁻ʳ dr]
= -r²e⁻ʳ + 2[-re⁻ʳ + ∫e⁻ʳ dr]
= -r²e⁻ʳ + 2[-re⁻ʳ - e⁻ʳ]
= -r²e⁻ʳ – 2re⁻ʳ – 2e⁻ʳ |[0 to Ω]

Hence, the integral from 0 to Ω is:
= F(b) – F(a)
= -Ω²e^(-Ω) – 2Ωe^(-Ω) – 2e^(-Ω) – [-0²e⁻⁰ - 2(0)e⁻⁰ - 2e⁻⁰]
= -Ω²e^(-Ω) – 2Ωe^(-Ω) – 2e^(-Ω) – [ -2]
= -Ω²e^(-Ω) – 2Ωe^(-Ω) – 2e^(-Ω) + 2

We now have the definite integral. Now, we must take the limit of this thing as Ω approaches infinity.
lim -Ω²e^(-Ω) – 2Ωe^(-Ω) – 2e^(-Ω) + 2
Ω→∞

Let’s apply some logic. As Ω approaches some very large number, the e’s are raised to very large negative numbers, making them approach 0. Thus, all terms multiplied by e^(-Ω) will approach 0. So we’re just left with:
= 0 – 0 – 0 + 2
= 2 (Answer)

Hooray! After all those solving, we got a very satisfying number as an answer! Hope this article helped those guys studying Calculus, and if you happen to see the person who solved or participated in solving these three problems at Yahoo! Answers, I am that guy. Hope this helps!